引入

这学期的一门课，虽然是材料系老师上的，不过 coding 工作量确实不小，还是比较花时间的。总结这些浪费的时间，很多时候其实不是花在编程上的时间，单单编程还是很快很机械的。

大部分的科学计算，比如计算物理，计算化学，难度不在编程，在于算法和背后的物理。比如今天这篇博文总结的问题就是如何更好的实现对于模拟体系的物理化学性质的统计。

首先还是规定下讨论的背景，前一篇博文分子动力学计算的小细节 是尝试构造一个可用的 LJ 液体体系。现在如果我们给系统设定一个很高的温度， 比如 500K， 那么系统就应该从固态进入液态，再过一定的时间当系统在液态稳定之后，我们就可以抽样感兴趣的物理量并且进行统计了。

当然，这里用到的第一个假设是，遍历性假设，也就是我们认为时间平均等于系综平均，在刘维尔空间的抽样是足够的。这条是统计力学的基础假设，但是不是自然界的普遍真理，当然你一般是遇不到这个假设不成立的情况的。就如普通人很难遇到欧几里得几何的平行公设不成立的情况。

第二个假设是液体的性质是足够均匀的。当我这么说的时候，是说从长时间的角度看，各个状态的液体是均一的。如果不满足那就进入了非平衡体系的范围了，耗散力和熵发挥作用。当然在美好的基础物理中这些都不会发生。

那么对于一个液体我们关心哪些性质，主要是三个，这儿一个个地讨论。

g(r)

第一个是 g(r), pair correlation function。

这个公式的含义是，平均来看，从当前原子向四周不停的画球面，在球面上可能出现粒子的密度是多少。

平均来看是什么？

平均来看其实是说，对于每一个原子都应该嵌套下面的步骤进行一次。所以 g(r) 是对于整体 system 而言的。不是针对某个特定的点而言。

画球面是什么？

画球面，其实是通俗的说法，数学上就是不断的对于数密度做球面的微分。这个目的是为了准确反应疏密度的发散变化。

为什么是密度？

其实是为了把这个性质在各个系统之间做比较，考虑两个同样设置的系统只是大小不同，那么绝对量虽然不同，但是密度是一样的。

所以在 g(r) 其实是只是当前时刻的性质，换句话说是 snapshot 的性质，不需要累加。

0K 时固体 g(r)

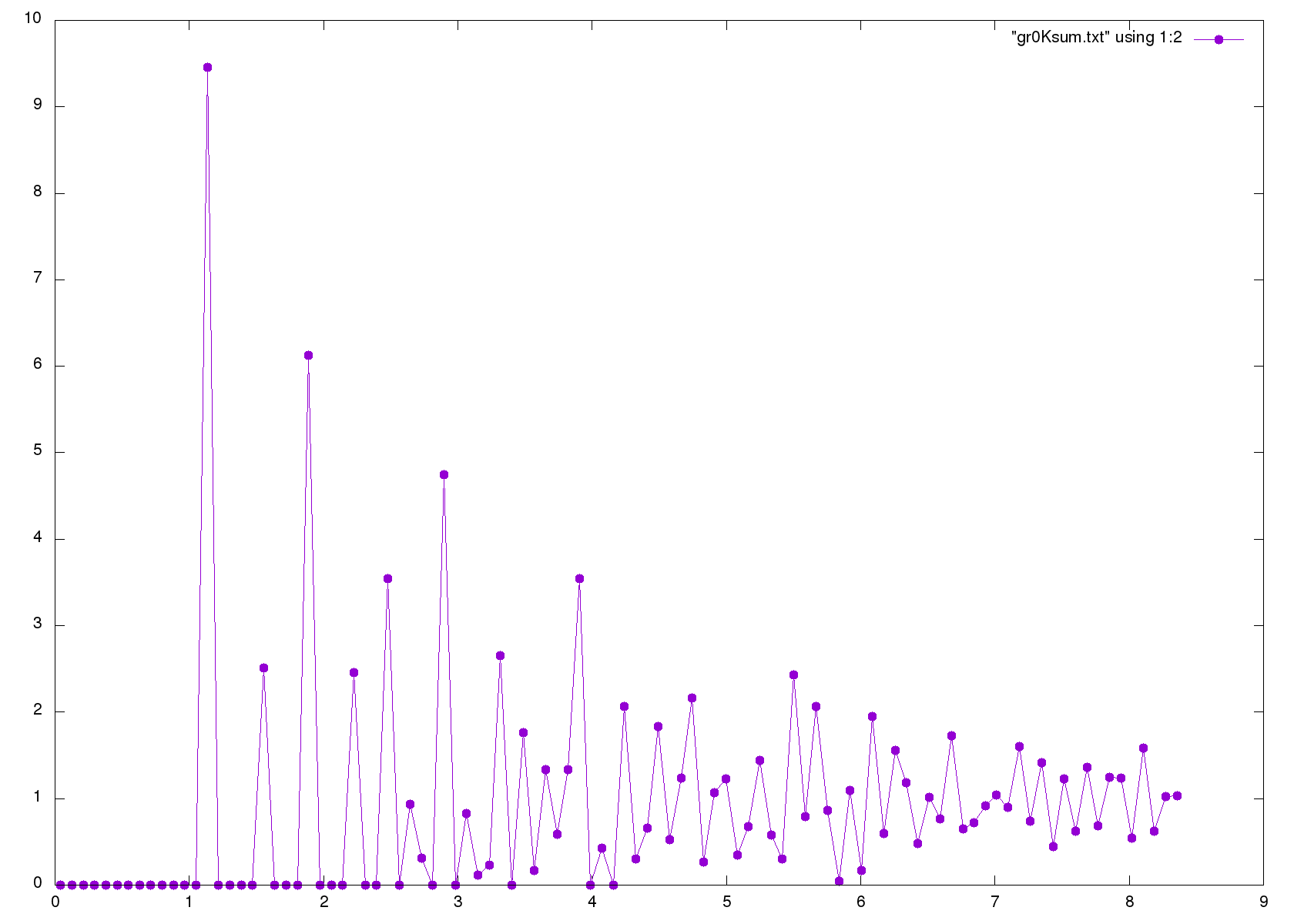
250K 时液体 g(r)

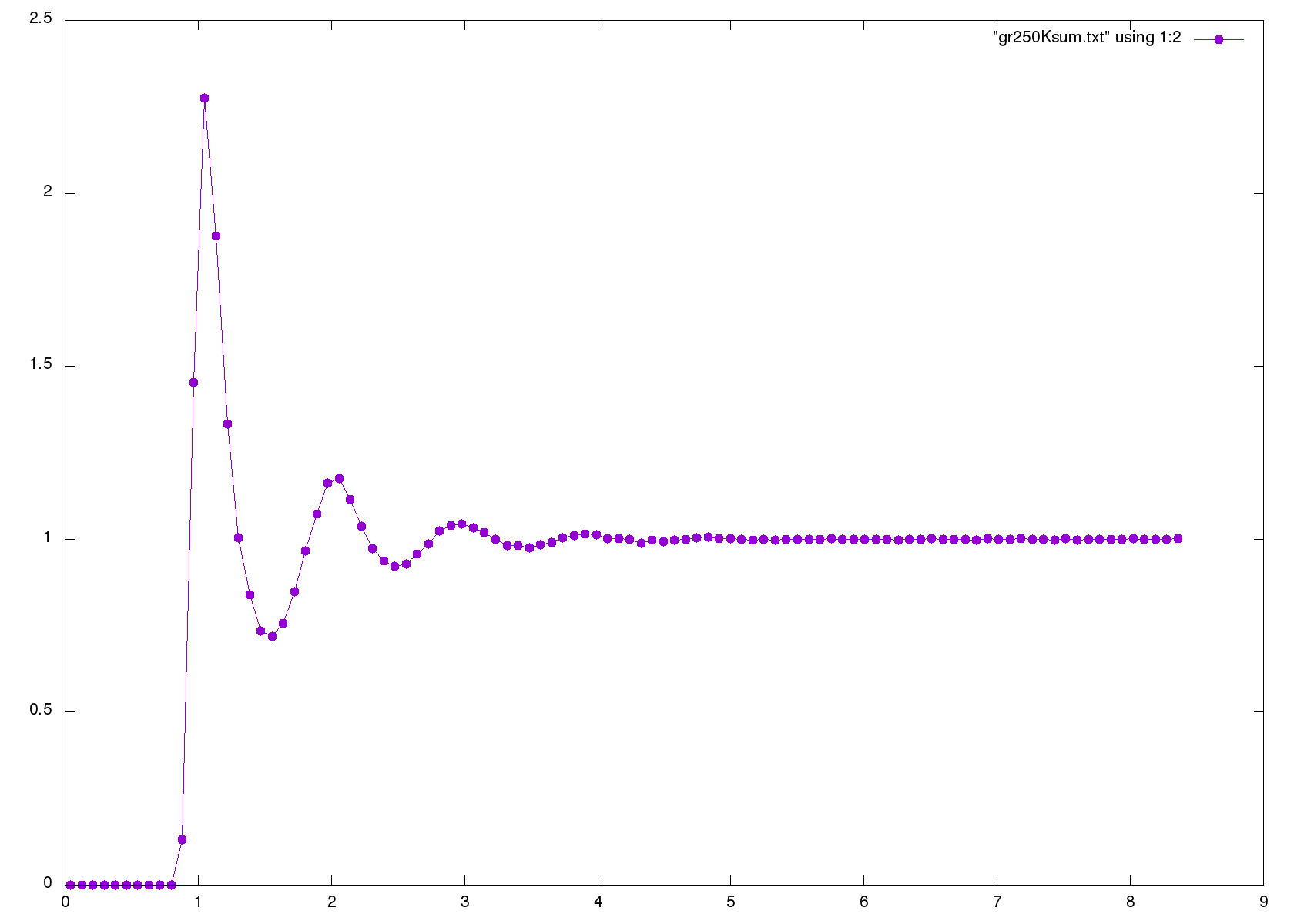
MSD

但是还有那么一大类性质是和时间相关的，换用术语就是需要从 trajectory 得到，比如 MSD, Mean squared displacement. 得到 MSD 最大的好处就是可以通过爱因斯坦关系，直接得到扩散系数，扩散系数是非常方便测量的物理量，所以可以很方便地和实验结果对比，从而判断模拟的好坏。所以 MSD 是常用的测量物理量。

\[{\rm MSD}\equiv\langle (x-x_0)^2\rangle=\frac{1}{N}\sum_{n=1}^N (x_n(t) - x_n(0))^2\]

几个注意点:

正好，读 Amber 的程序手册的时候看到一个很好的说明部分。写的非常清晰，关键就是我们知道在计算力和能量的时候周期性边界条件导致了对于距离的一个周期性选取。那么对于坐标需要不需要把运动位移拉回到一个体系原胞内部？

其实是不需要的，特别是在计算 MSD 的时候其实不拉回是比较好的选择。

具体原因就是，如果拉回，那么其实人为引入了一个约束，那就是两个粒子之间距离的最大差值不能大于你的周期性边界条件的作用范围。这是人为引入的一个假象，本质上是我们在计算机不够强大的条件下做的一个折中选择。

具体的说明如下:

下图是一张典型的 MSD 统计曲线

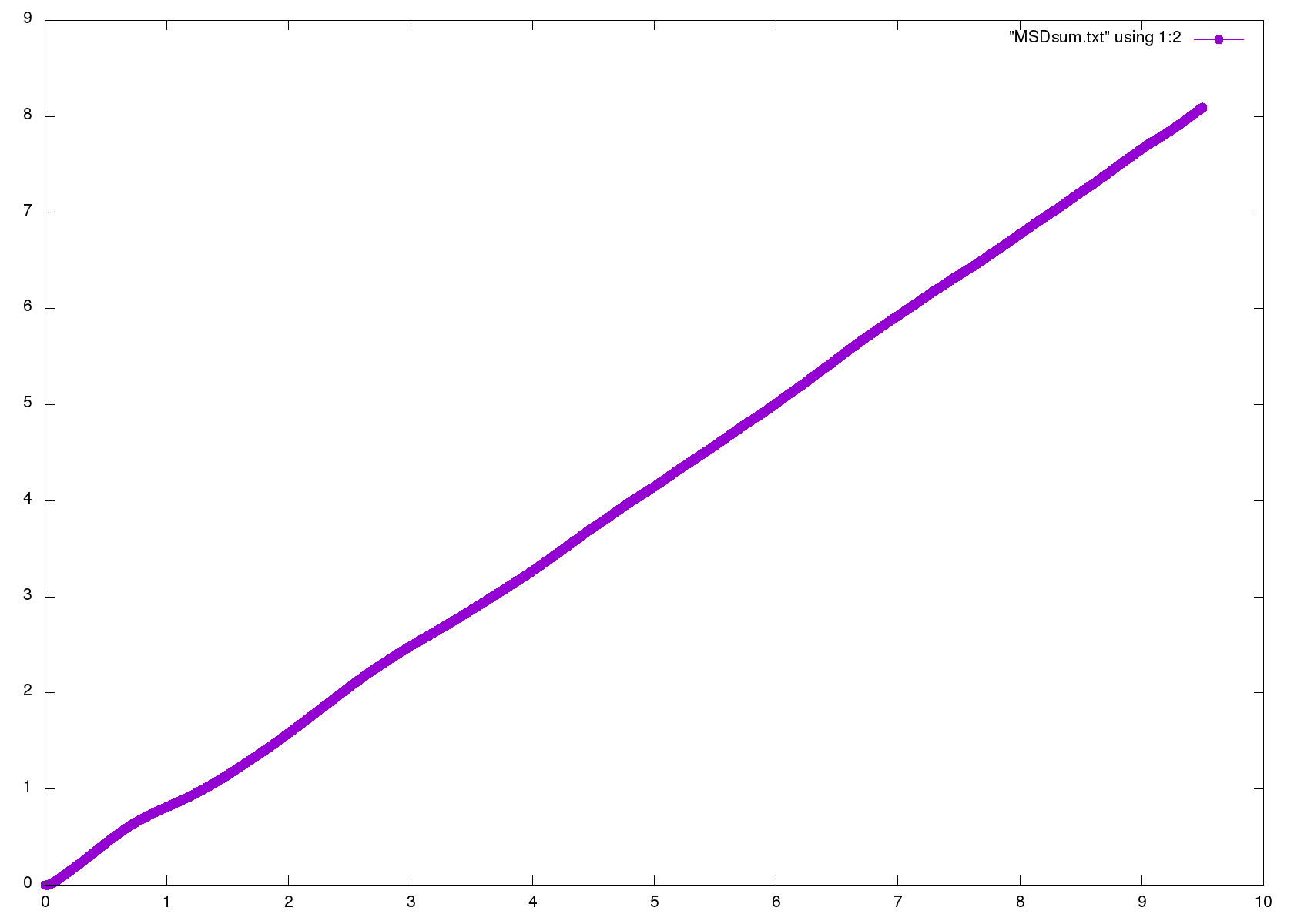
VAF

VAF就是velocity autocorrelation function (VAF) ，是关于速度的自相关函数。自相关函数是表达体系内在关联性质的重要函数。

所以 VAF 也是非常重要的性质，同时通过 Green-Kubo 关系, VAF 也可以和扩散系数联系在一起。

这里同样注意到 V0　必须取平衡后的时刻速度即可。同时，注意是 VAF 关于时间的积分和扩散系数关联，不是 VAF 本身。

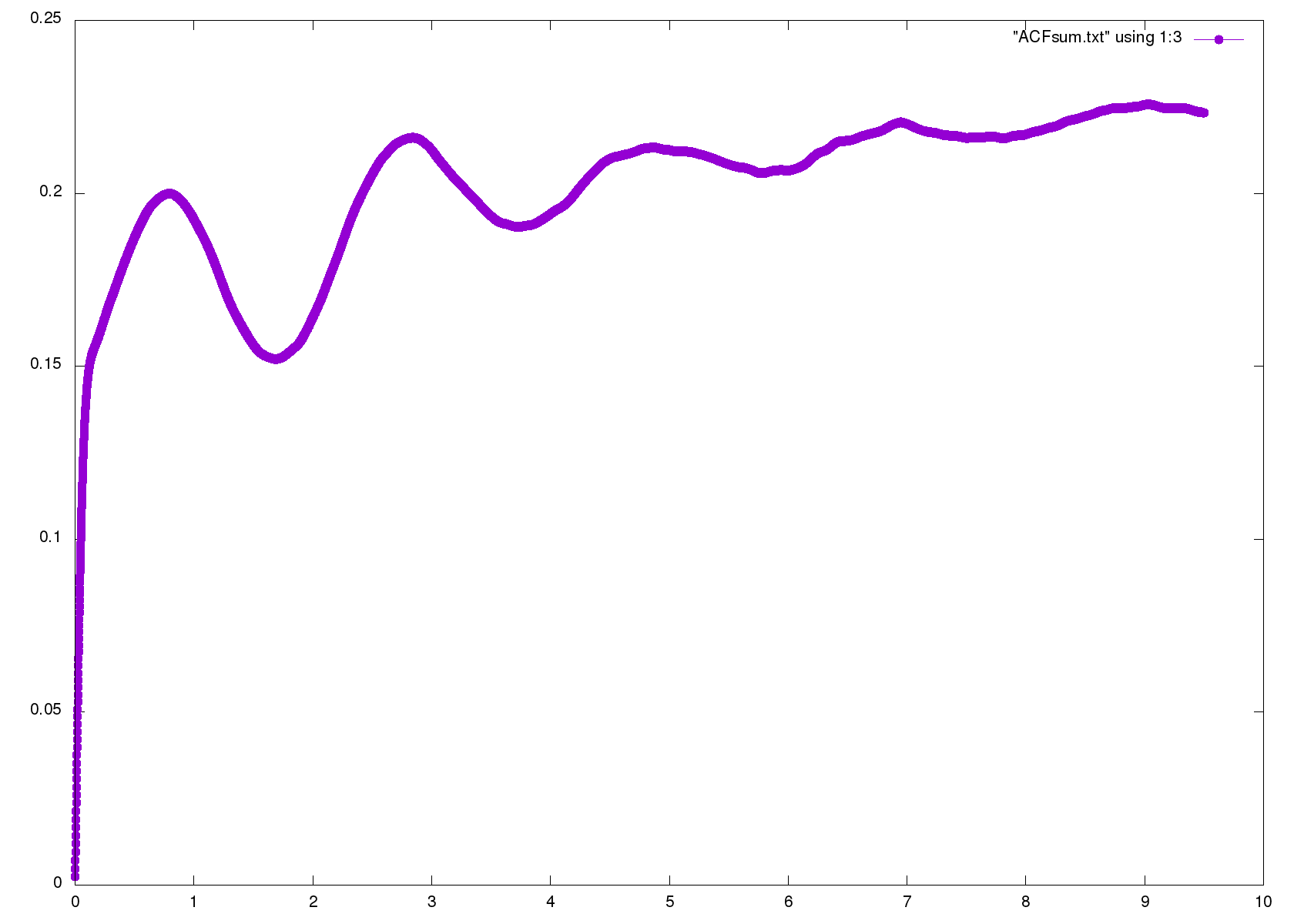
VAF 图像如下:

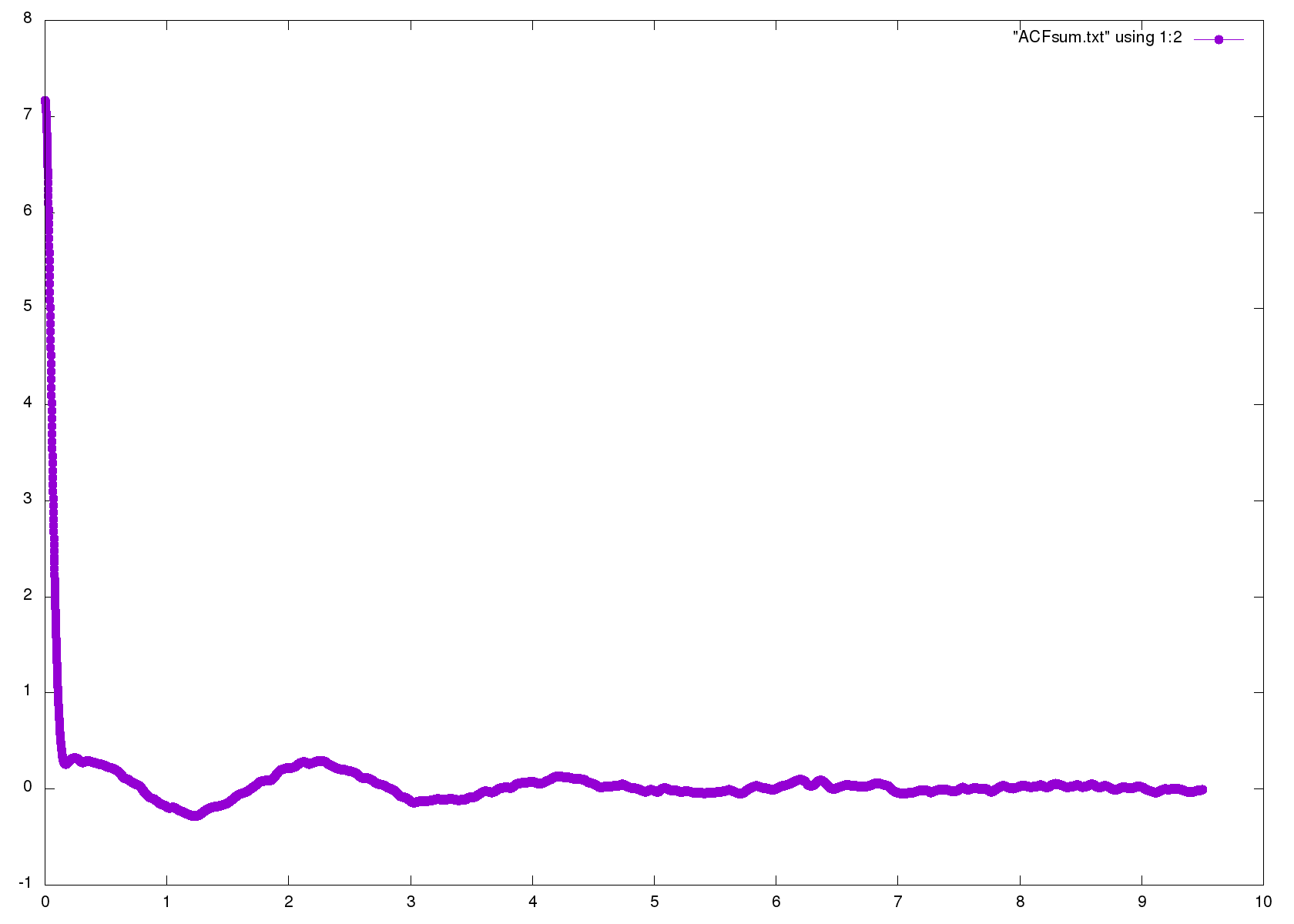
总 VAF 图像如下: