用矩阵操作快速实现图像识别中 Bounding Box 的准确率和召回率判断
起因
今天和同学一切讨论我们在做的项目,其中他特别指出了一段 Python 代码的精妙之处。我当时没能立刻理解,回来仔细思考了多次,终于想明白了这个问题,不由拍案叫绝。所以特地总结下这个问题给出自己的思考。
背景
像素坐标系
我们都知道,计算机图像是由像素点组成的。简单化的理解,忽略各种格式的区别,就是红色,绿色,蓝色三个通道的二维矩阵组合。一个通道是一个矩阵,这样在屏幕上,同一个像素点,三种颜色的混合就组成了一幅彩色图像。如下图所示
![]()
人看到的是色彩斑澜的图像,计算机看到的其实是一个填充了数字的矩阵。
Bounding Box
在图像识别的时候很重要的一个工作是通过 Bounding Box 把图像的大致区域框出来。在这一步并不需要每一个像素都精确区分,而是大致框出物体的范围。如下图所示:

那么问题来了,怎么表示这个 Bounding Box?
需要画出边框上的每个点吗? 显然不需要。
那最少需要几个?可以发现四个顶点是最特殊的,那四个都必须吗?显然也不需要。
最少我们只需要不是共线的两个顶点就行了,也就是互为对角线的顶点都可以。
习惯上我们取左上的点和右下的点(从人的角度看,暂时不考虑像素坐标系的方向问题)。
图像识别算法
如上面的 Bounding Box 图所示,其实图像识别算法就是对于任意一个输入的图像,考察是不是准确地预测出了 Bounding Box 的所在位置。当然为了让算法可以知道怎么学习,我们往往会事先通过 Bounding Box 标记出图像的位置,然后训练神经网络去通过学习图像的各种特征预测可能出现的Bounding Box 位置。
简单说,我们先标记一些 Bounding Box 然后我们的算法通过学习训练,最后实现对于一张未知图像的 Bounding Box 的预测。
precision(准确率) 和 recall(召回率)
这里就会有一个很自然的问题,我们怎么知道预测的准确还是不准确呢?
通常在机器学习算法中我们使用两个指标来表示算法的性能,precision(准确率) 和 recall(召回率)。简单说,用疾病检测举例,如果在 10000 人的检测样本中已知有 500 个阳性的病人需要预测出来,现在你设计了一个算法,预测了 400 个人是阳性,但是实际上这四百人里面只有 300 人是真的阳性(预测对了),其中 100 个人是阴性(预测错了)。所以你的准确率就是,基于你预测的 400 人,因为有 300 人是对的,所以准确率是 300 / 400 = 0.75。 换句话说准确率就是你预测的所有结果中有多少是对的。
召回率表示的是你预测的结果中对的部分到底覆盖了多少目标用户,可以看到我们的目标是预测出 500 个阳性病人,但是你预测的 400 人中只有 300 个是对的,所以你的召回率就是 300 / 500 = 0.6。简单说,召回率就是覆盖率,我们希望的好的算法能够在预测的时候覆盖更多的目标人群。
极端情况,如果你只预测一个人,同时这个人还是真是阳性,可以看到 准确率是 1 / 1 = 100%, 但是你的召回率只有 1/ 500 = 0.002 非常低。
另外的极端情况就是,你说所有人都是阳性病人,那么召回率就是 1。因为你把所有病人都包括了,你预测对的人是 500,同时你期望的目标人群是500, 500 / 500 = 1。换句话说,通过非常极端严格的筛查条件,宁可错误绝不放过,你成功实现了全覆盖。但是你的准确率低得令人发指,只有 500 / 10000 = 0.05。
所以在日常的使用中,我们往往是需要综合两个指标的。比较自然的指标有 F1 分数等。有兴趣的读者可以自行研究。
问题
问题的提出
我们集中到今天讨论的问题上,
假设对于某个图像,我的算法提出了自己预测的 N 个 Bounding Box,同时知道该图像的 M 个正确的 Bounding Box, 如何准备快速的计算 precision(准确率) 和 recall(召回率)?
下面我给出问题的预备代码和画图代码帮助大家理解这个问题:
import numpy as np
# create array data
predict = np.array([[1,2,2,1],
[4.5,2.5,2,1],
[6,6,8,4]], np.double)
truth = np.array([[1,4,3,3],
[5,2,8,1]], np.double)
# Below is to show the layout of the problem
# red represents truth
# blue represents prediction
import matplotlib.pyplot as plt
import matplotlib.patches as patches
fig = plt.figure()
ax = fig.add_subplot(111, aspect='equal')
recList = list()
# Adding blue rectangle from predict
for rect in predict:
recList.append(
patches.Rectangle(
(rect[0], rect[3]),
np.abs(rect[2] - rect[0]),
np.abs(rect[3] - rect[1]),
fill=False,
edgecolor = "blue"
)
)
# Adding red rectangle for truth
for rect in truth:
recList.append(
patches.Rectangle(
(rect[0], rect[3]),
np.abs(rect[2] - rect[0]),
np.abs(rect[3] - rect[1]),
fill=False,
edgecolor = "red"
)
)
# plot the graph
for p in recList:
ax.add_patch(p)
plt.plot()
plt.show()
fig.savefig('rect.png', dpi=90, bbox_inches='tight')
具体的图像如下;
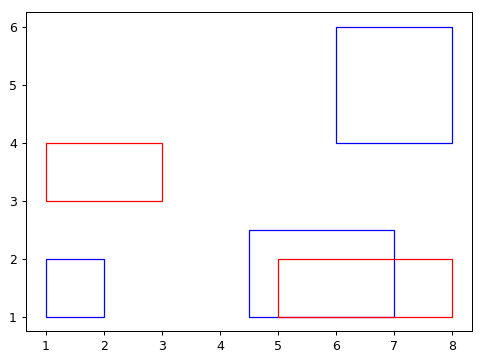
同时我们做一个简化,只考虑每个矩阵中心是不是在可以接受的误差范围内重合。相当于我们暂时只考虑位置不考虑大小。因为大小往往还会做后续的精细调节。大部分算法首先预测位置,然后大小到了需要的时候再进一步的细化。
计算中心可以使用如下的函数
'''
Calculate the center point of bounding box
'''
def bbox2centroid(bboxes):
return np.column_stack(((bboxes[:, 0] + bboxes[:, 2])/2, (bboxes[:, 1] + bboxes[:, 3])/2))
问题的思路
一个简单的思路就是逐个比较。这样的话你的算法需要写大量的循环非常费力。
所以,在实际的工作中,我们大量使用矩阵操作,避免循环。因为矩阵操作往往可以避免循环,同时如果你能够使用 GPU (通常图像识别都会在 GPU 上运行),矩阵操作本身是经过特别优化的,特别适合 GPU 运行,这可以提高速度。
但是怎么操作?
可以看到我特地给出了,预测 Bounding Box 数量和真实 Bounding Box 数量不一致的情况,所以这个时候如果不小心,非常容易出现矩阵的维度不匹配的情况那就毁掉了所有的计算。
所以我们可以用上面的例子来帮助思考,首先求中心的坐标,这样,原来的 \(N \times 4\) 矩阵和 \(M \times 4\) 矩阵就变成了 \(N \times 2\) 矩阵和 \(M \times 2\) 矩阵。
numpy 的 numpy.newaxis
这儿不得不说下,一个不太提及的小技巧。
在 numpy 中 None 也可以作为矩阵一个新的维度的占位符。用官方文档的说法,这叫做 numpy.newaxis
The newaxis object can be used in all slicing operations to create an axis of length one. :const: newaxis is an alias for ‘None’, and ‘None’ can be used in place of this with the same result.
也就是如果你希望你的矩阵拓展出一个新的维度,比如从一个长度为 3 的 vector 到 3 x 1 或者 1 x 3 你就可以这么写
A=np.array([1,3,5])
print(A)
print(A.shape)
print("====1====")
print(A[:,None])
print(A[:,None].shape)
print("====2====")
print(A[None,:])
print(A[None,:].shape)
输出是
[1 3 5]
(3,)
====1====
[[1]
[3]
[5]]
(3, 1)
====2====
[[1 3 5]]
(1, 3)
那么二维呢,新增加一个维度,用上面的写法,我们可以看到结果是:
A=np.array([[1,3,5],
[7,8,9]])
print(A)
print(A.shape)
print("====1====")
print(A[:,None])
print(A[:,None].shape)
print("====2====")
print(A[None,:])
print(A[None,:].shape)
输出是
[[1 3 5]
[7 8 9]]
(2, 3)
====1====
[[[1 3 5]]
[[7 8 9]]]
(2, 1, 3)
====2====
[[[1 3 5]
[7 8 9]]]
(1, 2, 3)
这样在 numpy 的操作中,如果需要增加一个额外的维度,比如存储两个矩阵做差的结果,就可以很方便将结果存储在新增加的这个维度,后面会更进一步解释。
也可以参考这个stackoverflowIn numpy, what does selection by [:,None] do?
问题的解决代码
这里我直接先给出代码。
'''
Calculating P and R function
'''
def compute_score_detail_by_centroid(pred_bbox, gt_bbox, tolerence=(2, 2)):
pred_c = bbox2centroid(pred_bbox)
gt_c = bbox2centroid(gt_bbox)
diffs = abs(pred_c[:, None] - gt_c)
x1, x2 = np.nonzero((diffs < tolerence).all(2))
precision = np.unique(x1).shape[0] / pred_bbox.shape[0]
recall = np.unique(x2).shape[0] / gt_bbox.shape[0]
return precision, recall
下面一步步解释下这个函数
(1) pred_c = bbox2centroid(pred_bbox) 和 gt_c = bbox2centroid(gt_bbox) 就是求 Bounding Box 的中心,在我们的例子中,做完这步操作, pred_c 是 \(3 \times 2\) 矩阵 而 gt_c 是 \(2 \times 2\) 矩阵。
其中 pred_c是
[[1.5 1.5 ]
[3.25 1.75]
[7. 5. ]]
gt_c是
[[2. 3.5]
[6.5 1.5]]
(2) pred_c[:, None] 将 \(3 \times 2\) 矩阵 扩展为 \(3 \times 1 \times 2\) 矩阵
(3) pred_c[:, None] - gt_c 是 \(3 \times 1 \times 2\) 矩阵 减去 \(2 \times 2\) 矩阵, 在数学上这是没有定义的,因为数学要求矩阵减法操作必须维度相同,但是在 numpy 中,其实是把 \(3 \times 1 \times 2\) 矩阵作为 3 个 \(1 \times 2\) 矩阵分别先扩充为 \(2 \times 2\) 矩阵 再和\(2 \times 2\) 的 gt_c 矩阵做减法。
也就是numpy 尽力将不能做的减法操作以第一个维度(你也可以指定其他维度)做减法操作。
所以这步结束我们得到一个 \(3 \times 2 \times 2\) 矩阵,沿着第一个维度,其中每一个小的 \(2 \times 2\) 矩阵都是预测的 Bounding Box 和真实的 Bounding Box 的中心差值。
具体的结果如下:
[[[0.5 2. ]
[5. 0. ]]
[[1.25 1.75]
[3.25 0.25]]
[[5. 1.5 ]
[0.5 3.5 ]]]
如果还是有一些疑问的话,请一行行调试如下的代码,我简单加了输出信息,
'''
Calculating P and R function
'''
def compute_score_detail_by_centroid(pred_bbox, gt_bbox, tolerence=(2, 2)):
pred_c = bbox2centroid(pred_bbox)
print(pred_c)
gt_c = bbox2centroid(gt_bbox)
print(gt_c)
diffs = abs(pred_c[:, None] - gt_c)
print(diffs)
print(diffs.shape)
x1, x2 = np.nonzero((diffs < tolerence).all(2))
print((diffs < tolerence).all(2))
print(np.nonzero((diffs < tolerence).all(2)))
precision = np.unique(x1).shape[0] / pred_bbox.shape[0]
recall = np.unique(x2).shape[0] / gt_bbox.shape[0]
return precision, recall
(4) (diffs < tolerence).all(2) 这步就是把上面求出来的 \(3 \times 2 \times 2\) 矩阵 和 我们允许的误差矩阵((2, 2))做比较,如果小于误差计作True,否则计作 False。但是这样结束之后我们得到一个\(3 \times 2 \times 2\) 的布尔(Boolean)矩阵。
[[[ True False]
[False True]]
[[ True True]
[False True]]
[[False True]
[ True False]]]
分别表示对于每一个预测的 Bounding Box ,它的 x 中心和 y 中心是不是在允许的误差范围内。我们知道如果都在范围内,那么就是预测对了,反之只要一个不对,那就是预测不对。
所以.all(2) 其实就是沿着第三个轴(Python从0计数)对于每一个元素是不是都是True,Test whether all array elements along a given axis evaluate to True.
那么第三个轴是哪个轴?
其实在我们说 差值布尔矩阵是 \(3 \times 2 \times 2\) 矩阵 就说明了第三个元素是第二个 2 ,也就是对于布尔矩阵沿着每个小列做操作。正好就是对于每个x轴中心误差和y轴中心误差做逻辑AND操作。通过这个操作之后,我们发现现在布尔矩阵变成,
[[False False]
[ True False]
[False False]]
现在是 \(3 \times 2\) 的矩阵了,相当于沿着第三个轴塌缩了。
现在的结果就是,对于我们的每一个预测(一共 3 个预测)我们分别和真实值( 两个真实值 )做对比,得到一个判断结果分别是 True 还是False,我们可以看到第二个预测 Bounding Box 和第一个真实 Bounding Box 是吻合的。结合我们的图,会发现正好是右下角重合的两个矩形。

(4) x1, x2 = np.nonzero((diffs < tolerence).all(2)) 主要需要理解np.nonzero(),其实就是返回每一个维度的非零元素,在我们这个布尔矩阵中就是返回每个维度的True数目。Return the indices of the elements that are non-zero.Returns a tuple of arrays, one for each dimension of a, containing the indices of the non-zero elements in that dimension.
但是在这儿x1和x2的含义不太明确。所以下面我进行一次形式化的论证。
可以看到在得到中心坐标后,我们的问题是
\(N \times 2\) 的预测矩阵和 \(M \times 2\) 真实值矩阵的差是不是在允许的范围内。
所以在扩展一个维度后,变成\(N \times 1 \times 2\) 的扩展预测矩阵和 \(M \times 2\) 真实值矩阵做差。然后对于每一个预测 Bounding Box 的中心,一共是\(N\) 个,在新扩展的维度上和 \(M \times 2\) 真实值矩阵做差。所以每一个预测 Bounding Box 的中心 ( \(1 \times 2\) ) 先扩展成 \(M \times 2\),就是把单一行复制为 \(M\)行,得到每行元素相同的一个 \(M \times 2\) 矩阵, 再和 \(M \times 2\) 真实值矩阵做差。
所以我们到的布尔矩阵是 \(N \times M \times 2\) 的矩阵,其中第三个轴的第一个布尔元素代表 X 方向是不是在误差内,第二个布尔元素代表 Y 方向是不是在误差范围内,然后再沿着第三个轴做all操作,所以我们得到 \(N \times M\) 的矩阵,其中每一行都是代表一个预测 Bounding Box 的中心 是不是和 \(M\) 个真实 Bounding Box 的中心重合。
所以 x1 得到N中的True数目而x2得到M中的True数目。所以结合上面 precision(准确率) 和 recall(召回率) 的定义,我们知道 x1 就是 precision(准确率) 而 x2就是 recall(召回率)。
当然为了得到具体的数值,还需要做进一步求解,不过已经非常简单了, 也就是最后的几步。
总结
可以看到这个对于这样一个简单的问题,通过充分利用 numpy 内置函数的特性和矩阵操作的便利,特别是增加一个维度实现对于另一个矩阵的遍历实现具体的机器学习precision(准确率) 和 recall(召回率) 计算。
这是特别值得学习的操作。
