用影子数组 ( Shadow Array )加速数组扩容
起源
这学期学习数据结构,其中一个概念想了很久,就是影子数组的问题。
Shadow Array
影子数组主要的作用是帮助实现在扩增的时候,实现快速的迭代。因为比较难以用语言形容,这里我直接用纸币来解释问题了。
影子数组其实就是就是在每一个数组实现中都同时实现一个两倍于当前数组的数组。这样在实现的时候,每一步都同步拷贝新的元素到影子数组,当当前数组满了的时候直接切换到影子数组,这样实现原来数组满了之后会出现的 O(N) 时间到常数时间。
用下图表示:
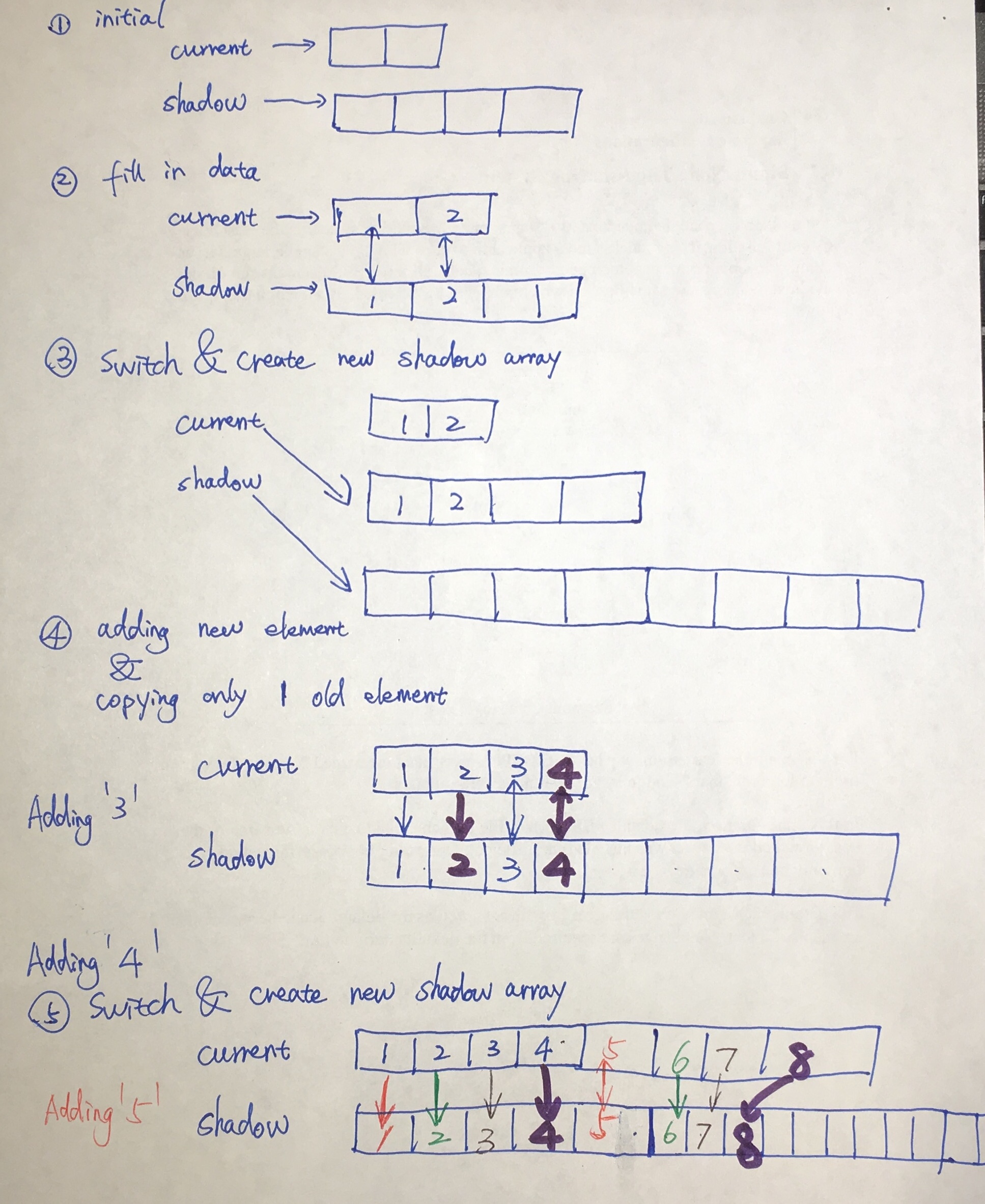
1. 创建 current 和 shadow 两个数组
我选择 2 作为初始的大小吗,所以 current 的长度是 2 , shadow 的长度是 4。
2. 填充元素
分别在每一步同时拷贝新元素(1,2)进入 current 和 shadow 两个数组。
3. 切换数组并建立新数组
可以看到当当前数组满了之后,我们切换 current 到 shadow,然后重新建立一个两倍大小的心 shadow。原来的 current 会有JVM回收,不用担心。
但是这个时候一个自然的问题,需要拷贝原始元素到新的 shadow 吗?
很显然,新的 shadow 是空的,我们需要拷贝,但是不应该选择一次性到位。因为这样又需要把原数组遍历一边,时间复杂度还是 N (对于添加新元素这步操作而言)。
4. 添加新元素 并 一次拷贝一个老元素
可以看到,当添加新元素 3 的时候,除了把 3 拷贝到它所在的位置上,同时我们拷贝了current 数组的第一个元素 1 来填补 shadow 数组缺少的第一个元素。
相应的做操作添加新元素 4。
这时候发现 current 又满了,需要切换了。同时我们发现,因为新的数组始终是两倍扩大,所以其实当空的一般填满了,多复制的旧元素也把新 shadow 补足了。
5. 切换数组并建立新数组
这步其实就是说明这个操作的可行性,可以看到当 current 满了,需要切换的时候,每次 shadow 也正好补满。
同时因为每步拷贝做一个添加新元素加上拷贝旧元素的操作,时间复杂度不变还是 O(1) 量级。
思考
其实这里最重要的思想就是,不要一曝十寒,要细水长流,把一个宏大的任务分解掉。其实总的操作数不变,但是每一步的 workload 就比较均衡了。
但是,实现这个前提是,你的数据结构比较精巧。
可以看到每次都扩大两倍是最好的选择,如果每次扩大三倍,就不能保证这个操作的完整性和方便性。
实际工程
当然上面的结果都是理论的推到,实际中用的每次扩大 2.5 倍而不是 2 倍。
具体
- In Java, ArrayList uses x = 3/2.
- In C++, the GCC STL implementation uses x = 2.
这个呢,其实没什么道理,只是某种工程实践指导下的选择,因为这样可以降低 resize 的次数。
可以看下下面两篇文章的讲解。
Why Java grows ArrayList by 3/2?
